힙 heap 자료구조 파이썬으로 알아보기

힙은 트리가 완전한 이진 트리인 특별한 트리 기반 데이터 구조다.

힙은 트리가 complete(완전) binary(이진) 트리인 트리 기반의 자료구조이다. 일반적으로 힙은 다음 두 가지 유형으로 구성될 수 있다.

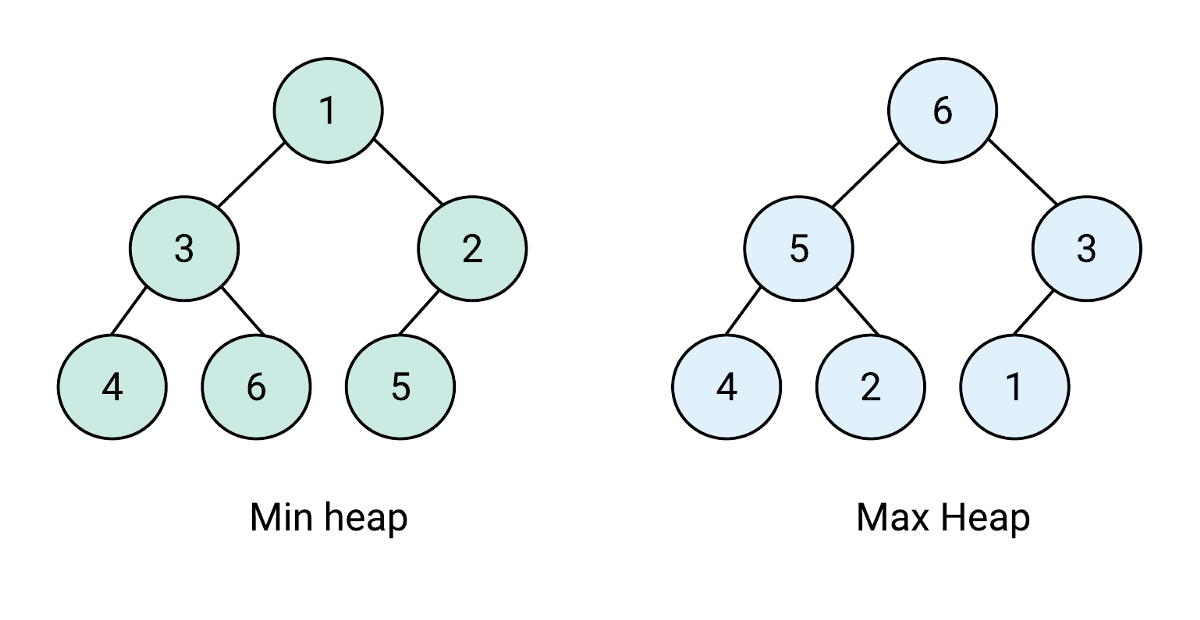
• Max-Heap 최대힙: 최대 힙은 모든 자식들보다도 루트인 노드가 가장 큰 값을 가지고 있는 트리이다. 그 아래의 sub-tree들에도 재귀적으로 같은 속성을 갖는다.
• Min-Heap 최소힙: 최소 힙은 모든 자식들보다도 루트인 노드가 가장 큰 값을 가지고 있는 트리이다. 위와 같은 원리이다.

 

 

Heap queue (or heapq) in Python

힙 데이터 구조는 주로 priority queue를 나타내는데에 사용된다. 파이썬에서, heapq 모듈을 사용 가능하다. 

Heap에서의 다양한 작업들:

• heapify(iterable) - iterable에서 heap 자료구조로 바꾸는데 사용된다.
• heappush(heap, ele) - 힙 자료구조에 element를 삽입하는데 사용된다. 힙 자료구조의 특성을 유지하기 위해서 순서는 재 조정된다. 

# importing "heapq" to implement heap queue 
import heapq 
  
# initializing list 
li = [5, 7, 9, 1, 3] 
  
# using heapify to convert list into heap 
heapq.heapify(li) 
  
# printing created heap 
print ("The created heap is : ",end="") 
print (list(li)) 
  
# using heappush() to push elements into heap 
# pushes 4 
heapq.heappush(li,4) 
  
# printing modified heap 
print ("The modified heap after push is : ",end="") 
print (list(li)) 
  
# using heappop() to pop smallest element 
print ("The popped and smallest element is : ",end="") 
print (heapq.heappop(li))

 

Output

The created heap is : [1, 3, 9, 7, 5]

The modified heap after push is : [1, 3, 4, 7, 5, 9]

The popped and smallest element is : 1

 

heappush 의 다른 방법:

>>> h = []
>>> heappush(h, (5, 'write code'))
>>> heappush(h, (7, 'release product'))
>>> heappush(h, (1, 'write spec'))
>>> heappush(h, (3, 'create tests'))
>>> heappop(h)
(1, 'write spec')

>>> import heapq
>>> a = [2, 5, 3, 7, 6, 8]
>>> heapq.heappush(a, 4)
>>> a
[2, 5, 3, 7, 6, 8, 4]
>>> heapq.heappop(a)
2
>>> heapq.heappop(a)
3
>>> heapq.heappop(a)
4

heapsort

>>> def heapsort(iterable):
...     h = []
...     for value in iterable:
...         heappush(h, value)
...     return [heappop(h) for i in range(len(h))]
...
>>> heapsort([1, 3, 5, 7, 9, 2, 4, 6, 8, 0])
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]